北理工大學在Stokes流體研究方面取得重要進展
發布日期:2021-05-12 供稿:數學與統計學院
編輯:陶思遠 審核:田玉斌 閱讀次數:
在Stokes流體方程中有一個長期懸而未解的數學問題---流體的Kac問題:能否通過測量Stokes流體振動時發出的頻率就能夠判斷出這片流域的體積和表面積?通俗地說:希望能通過測量一片流域的“波濤聲調”來判斷這片流域的大小。日前,北京理工大學數學與統計學院劉跟前教授在線發表于國際權威數學期刊《Mathematische Annalen》上的一篇論文《The geometric invariants for the spectrum of the Stokes operator》對這一問題給予了肯定的回答,從而徹底地解決了這個著名的流體Kac問題。
劉跟前教授用了偏微分方程、微分幾何、擬微分算子理論、奇異格林算子以及譜幾何理論的方法創造性地給出如下重要的譜漸近公式:
![]() .
.
這里![]() 是Stokes流的粘性常數,
是Stokes流的粘性常數,![]() 是Stokes算子的Dirichlet特征值,
是Stokes算子的Dirichlet特征值,![]() 是Stokes流的體積,
是Stokes流的體積,![]() 是Stokes流的表面積。而
是Stokes流的表面積。而![]() 是相應于
是相應于![]() 的特征向量,亦即
的特征向量,亦即
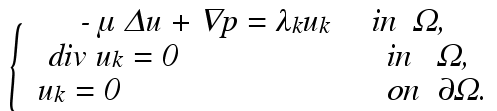
這個公式表明:知道了Stokes流的所有振動頻率,就可以通過它計算出流體的體積和表面積。由此徹底地解決了流體Kac問題。這個公式也建立了(物理)頻譜量和(數學)幾何量之間的緊密聯系。另一方面,這一公式具有重要實用價值。例如,在航海、石油及水資源探測、軍事等領域可以應用這一公式測量流域的大小。
該論文長達48頁,從投稿、專家審稿到被該雜志接受長達四年時間,兩位審稿人對劉跟前教授的論文給予了高度評價,一致認為該論文是“very interesting and actual”.
論文鏈接:
https://link.springer.com/article/10.1007/s00208-021-02167-worhttps://doi.org/10.1007/s00208-021-02167-wor as a PDF here
https://link.springer.com/content/pdf/10.1007/s00208-021-02167-w.pdf.
作者簡介:
劉跟前,北京理工大學數學與統計學院教授、博導,長期從事偏微分方程、幾何分析、譜幾何和反問題等領域的研究,在《Advances in Mathematics》等國際數學權威期刊發表一系列重要論文,解決了若干長期懸而未解的公開問題,其中包括解決了雙調和Steklov特征值的Weyl律、雙曲空間上高階Sobolev不等式、彈性特征值的Avramidi等問題。
分享到:
